弧度法
「弧度法」の授業は、2本の柱からなる。①「度数法」から「弧度法」変換させる、②扇形の弧の長さや、面積を求めさせる問題からなる。計算自体は簡単なので、抵抗なく進めることができる。しかし、弧度法にする理由が教科書に載っていない。教師の解釈でよいので、変換する理由を語れればよいと考える。
1 授業のアウトライン
① 教科書の例示問題1・練習問題1(25分)
➁ 例示問題2・練習問題2(15分)
③ 教科書傍用問題集(10分)
2 教科書の例示問題1・練習問題1はこう授業する
この項の柱は①弧度法、②扇形の弧の長さと面積の2本立てである。
➀弧度法
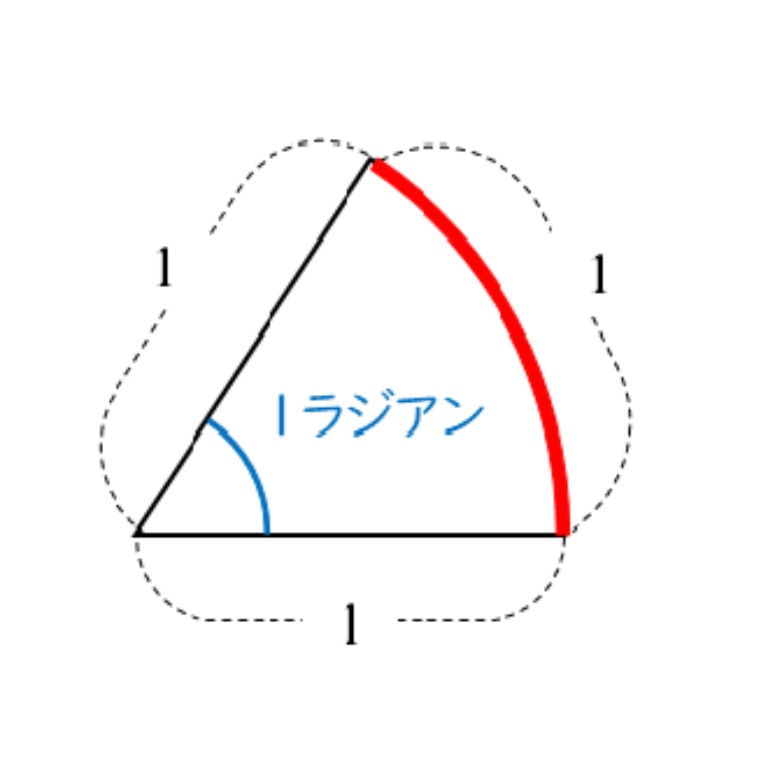
教科書104ページ。『弧度法』を読みます。
正三角形のように、動径が1、弧も1です。中心角は60°より大きいですか、小さいですか。(小さいです)(考えた理由も聞くとよい)
教科書の1ラジアンの図をかきます。(分度器を使ってかかせるとなおよい)

円周は2\pi:360°。半円はなんてかけますか(\pi:180°です)
「まとめをかきます」
また「度数法」⇔「弧度法」に変形させる方法も教えたい。
「度数法」→「弧度法」:×\frac{\pi}{180°}
「弧度法」→「度数法」:×\frac{180°}{\pi}
この授業に直接関係ないが、「弧度法のメリット」を伝えることもあとで必要になる。
私は
① 「長さ」がそのまま「角度」になる
② 扇形の弧の長さと面積が求めやすい
と伝えている。
3 例示問題2・練習問題2はこう授業する
② 扇形の弧の長さと面積
ここはそれほど難しくないので、教科書を読ませ公式を確認する程度でよい。
「教科書105ページ。冒頭から読みます」「[弧の長さℓ]を読みます」
式をそっくりそのまま写します。(ここは、公式の成り立ちに触れさせる程度でよい)
「[面積S]を読みます」
式をそっくりそのまま写します。(ここは、公式の成り立ちに触れさせる程度でよい)
なぜ、\frac{1}{2}r^2 \theta が\frac{1}{2}r ℓになるのですか。(r \theta =ℓ だからです)
面積Sの式は両方覚えさせる。
「かき終わった人から、公式を唱えていなさい」(後に指名して、暗記しているかを確認する)
